Is this the idea Mr. Corné Quartel wants to convey?
 |
 |
 |
1 |
2 |
3 |
 |
 |
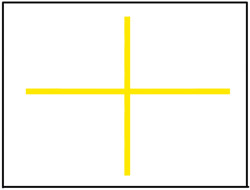 |
Still veiled by the outer form of a landscape or a building, horizontal (1) and vertical (2) merge in the figure of a tree (3).
 |
 |
 |
4 |
5 |
6 |
 |
 |
|
We find the same pattern (the basic structure of a tree) in the center of an abstract composition (4).
All around the central rectangle horizontals and verticals generate a variety of ever changing relationships while the basic pattern remains steady in the center.
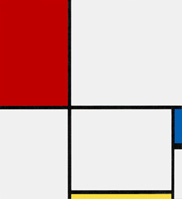
Five years later (5) we see an analogous idea expressed through color: yellow, red and light blue small rectangles give birth to a variable and manifold space which finds moments of relative steadiness when four small rectangles join together to form larger units of the same color. In the upper central area we note a white larger rectangle surrounded by three yellow, red and blue larger rectangles.
6: In a different way a white rectangle is surrounded by yellow, red and blue planes here too.
Compared with 5 the composition presents now fewer elements and has become asymmetric; each plane is now different not only in terms of color but also in terms of size and proportions.
 |
|
7 |
5 |
After a long period of compositions made of fewer elements (1921-1932). The manifold space of 4 and 5 re-appears in a new form with Broadway Boogie Woogie in 1942 (7) At first sight and on a quite superficial level one could see faint analogies between the schematic rectangles of 5 and those of 7 whose measures and proportions, however, differ from one another.
 |
 |
|
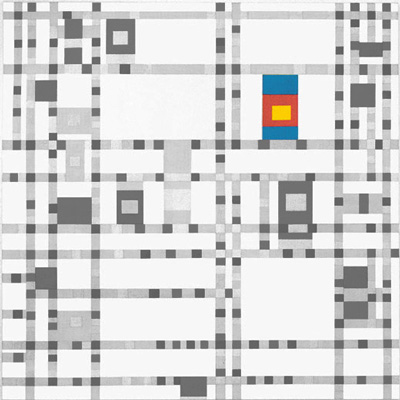
7 - Detail |
5 - Details |
An increased similarity can be seen between the yellow, red and blue plane of 7 and two large vertical areas formed by six small rectangles we see in 5, once made of red and yellow and once made of blue and red.
This is of course a gross interpretation. For an explanation of 5 see here. For an explanation of 7 see here.
|
8 |
In Victory Boogie Woogie, Mondrian's last unfinished canvas, we finally see the largest number of different rectangles of various shapes and colors which give birth to a dynamic, asymmetric and very subtle space.
Of course the evolution process from 1, 2, 3 up to 4, 5, 6, 7, 8 is much more complex than this. See here.
Copyright Michael (Michele) Sciam 1989-2021 |

